原文链接：https://mp.weixin.qq.com/s/MSxS63Ff1Me52xHUmLrm4g

线上实验课中，在展示卷褶伪影出现的原因时，有同学提出：为什么是左侧溢出部分卷褶到右侧，右侧溢出部分卷褶到左侧，即对侧卷褶特性？这个问题涉及到数字信号处理中的时域和频域，离散和周期之间的对应关系，要解释起来不是很方便，所以只给出了原因：是由于时域的离散对应着频域的周期延拓所造成。现在从原理上给予详细阐述。

一、首先对卷褶伪影的表现进行说明

仿真实验平台上，当采用默认参数，Gx=Gy=1.1Gs/cm时，采集的k空间和重建图像如图1所示：

图1 采集的k空间和重建图像

由于MRI图像是空间频率域，即空间和频率是等效的，二者之间由系数K进行转换：f=k C；f为频率，C为空间坐标位置。具体到二维平面，横向位置有f_x=k_xX；纵向有f_y=k_yY。其中，k_x=𝛾G_x;k_y=𝛾G_y。因此SW=100KHz的视野频率范围，在Gx=1.1Gs/cm的梯度场下，选定的视野空间范围为：FOV_x=SW/𝛾G_x≈21.4cm（注1T=10000Gs）。

人脑模型的横向尺寸为20cm，在1.1Gs/cm的梯度场下，左右两侧的频率差为：Δf =𝛾G_xΔX≈93.6kHz，因此脑模型图像在横向上占视野的比例约为93.6kHz/100kHz=93.6%。频率和位置映射关系如图2所示。由此也进一步说明，磁共振图像是空间频率域的信号（空间和频率一体），原始K数据是时间域的。

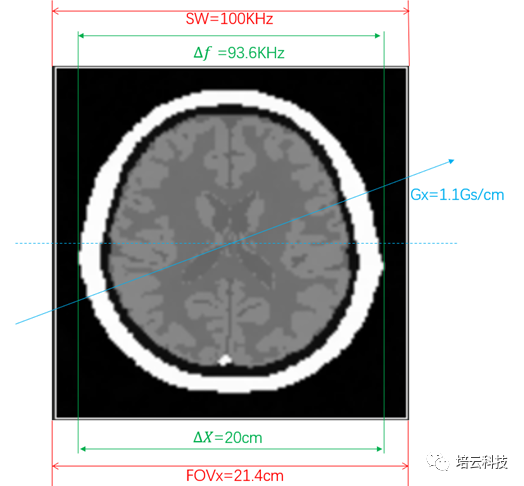
图2 频率编码方向的频率和位置映射关系

当采样带宽SW保持不变，分别调整三种梯度时：①Gx=1.6Gs/cm；②Gy=1.8Gs/cm；③Gx=1.6Gs/cm，Gy=1.8Gs/cm时，模拟采集得到的图像如图3所示，分别出现横向、纵向和横纵向的卷褶伪影。卷褶伪影出现的原因是，梯度过大，样品尺寸的左侧和右侧的自旋核产生的频率差，比决定视野范围的SW还要大时，超出的频率部分信号被卷褶到SW范围内了。根据频率和空间的映射关系，空间上也体现出图3所示的卷褶效果。

图3 不同的频率编码和相位编码梯度场下的卷褶伪影表现

仔细观察会发现，其卷褶是对侧进行的（图4所示），即左侧溢出的部分会卷褶到右侧，而右侧溢出的部分卷褶到左侧。同理，上下侧卷褶也是同样的。那么为什么必须是对侧卷褶的？很欣慰有好学的学子线上提出这个值得深究的问题。

图4 卷褶伪影的对侧卷褶特点

二、时域信号离散采样后的频域周期延拓性

这里以图示的形式做一个简单的表象过渡和物理含义。不阐述其数学原理。

1. 时间域为连续非周期信号

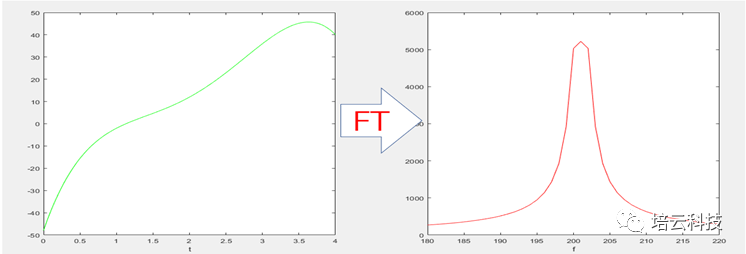
图5  连续非周期时域信号（左图），其频谱也是连续且非周期的（右图）

其物理含义：非周期性的时域信号，由一段连续频率范围的正弦波叠加而成。或者说，一段连续频率范围的正弦波可以合成出一个非周期性的时域信号。

2. 时间域为连续周期信号

图6 连续周期时域信号（左图），其频谱是离散且非周期的（右图）

但当时域信号体现出周期特性时，其频谱就变得不再连续的，而是某些离散频率的。其物理含义：周期时间信号，可以看成是一些离散频率的正弦波叠加而成的。故傅里叶级数的计算前提是时域信号必须是周期的，也就是说，只有周期的时域信号才能计算其傅里叶级数，非周期的时域信号只能做傅里叶变换。

3．时间域为离散非周期信号

将前述的时域连续非周期信号，经采样变成离散信号。其频谱是连续的，但进行了周期延拓，即时域信号的离散对应着频谱信号的周期延拓。延拓周期为采样时间间隔Ts的倒数（采样频率）。其物理含义是：信号经过离散采样后，原信号的频谱将以采样频率为周期进行周期拓展。

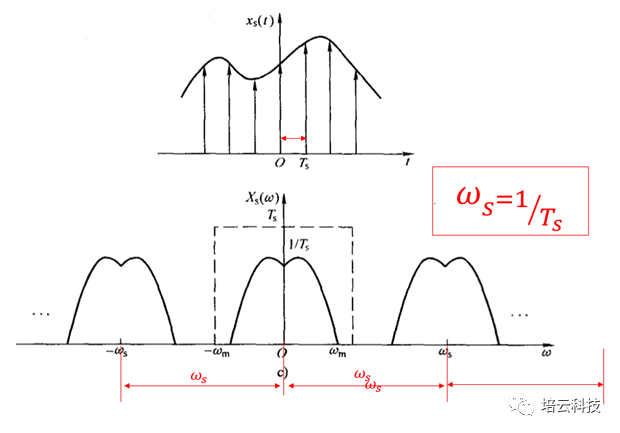
图7 连续非周期时域信号，经采样后，连续频谱产生周期延拓

4. 时间域为离散周期信号

同理，离散且周期的时域信号，那么频谱将是离散且周期延拓。

5.总结

综上可知，时域和频域之间存在着周期与离散，连续与非周期的互换对应性，如下：时域的连续对应着频域的非周期；

           时域的离散对应着频域的周期；

           时域的非周期，对应着频域的连续；

           时域的周期，对应着频域的离散。

这种对应性在数字信号处理和信号与系统课程中是基础性质。组合起来总结如下表：

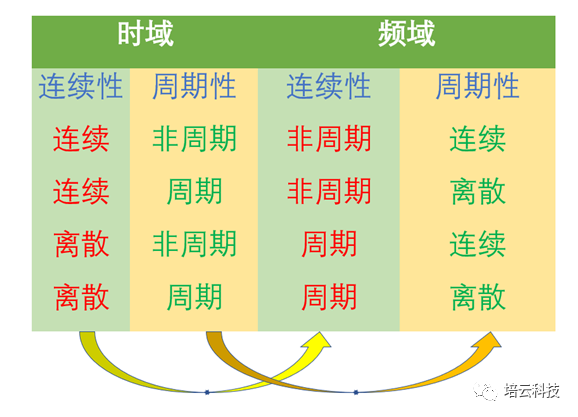
表1 时域和频域的互换特性

上表展开，是四个方面的内容：

（1）连续非周期的时域信号，其频谱是非周期连续的；

（2）连续周期的时域信号，其频谱是非周期离散的；

（3）离散非周期的时域信号，其频谱是周期连续的；

（4）离散周期的时域信号，其频谱是周期离散的。

三、卷褶伪影的对称卷褶原因

再回到MRI的卷褶伪影，对应着上述的第（3）项：离散非周期的时域信号，其频谱是周期连续的。MRI原始数据是非周期的，经离散以后，频谱会出现周期延拓。

基于MRI图像是频率分布的基本概念，结合离散采样会导致频谱周期延拓的性质，可知：当样品的信号频率范围大于采样带宽时，离散采样后的周期延拓，使得高频部分卷入了低频一侧，而低频部分卷入了高频一侧。由于MRI图像的频率和空间是一致（即通过系数k实现比例变换）的，因此体现出左侧溢出部分卷褶到右侧，而右侧溢出部分卷褶到左侧的表现。

由此可知，出现卷褶伪影的原因，从空间域角度讲，是设定的FOV小于样品的尺寸。从频域角度讲，是因为采样带宽范围小于样品的实际频率范围。二者本质上是一回事，中间差一个k系数的映射而已。再说得本质一点，是没有满足奈奎斯特采样定律：采样至少要大于待采样信号最高频率的2倍，否则会出现频谱的卷褶失真。如图8所示，当样品的频谱fmax大于采样带宽（SW）的一半时，周期延拓的频谱就被卷褶进来。

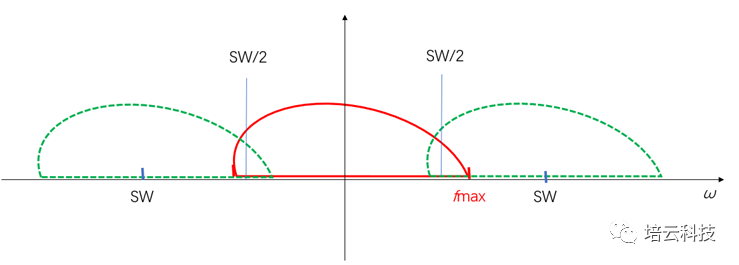
图8 样品频谱范围（红色）超过采样带宽时，会出现频谱卷褶

最后用三张经典的卷褶伪影临床图像作为结尾，对照着图像，回顾一下卷褶伪影的特点和原因。

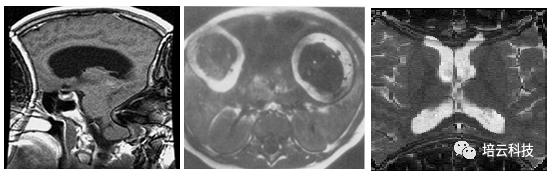
图9   卷褶伪影：左, 出现在脑部矢状面频率编码方向; 中：出现在胸腹部横断位频率编码方向（两只手臂卷褶到腹部中）；右, 出现在脑部横断位相位编码方向。

题后语：

为便于理解，以上仅从信号表现和物理含义的角度进行了说明，严格的论证需要从数学角度阐述。

磁共振成像难于理解有多方面原因，其中之一是学科综合性特点，比如这部分知识是《数字信号处理》和《信号与系统》课程的基本内容。但磁共振成像学习者，很少会先修这两门课程，所以本文作为选读内容，献给以弄清楚磁共振成像原理为乐的同学和同道。